ПОДОБЪЕКТ
- ПОДОБЪЕКТ
-
объекта категории — понятие, аналогичное понятию подструктуры математич. структуры. Пусть
— произвольная категория и А — фиксированный объект из
. В классе всех мономорфизмов из
с концом в Авводится отношение предпорядка (отношение делимости справа):
предшествует
или
, если m=m’s для нек-рого
. В действительности, морфизм m’ однозначно определен, поскольку s — мономорфизм. Отношение предпорядка индуцирует отношение эквивалентности между мономорфизмами с концом в А:мономорфизмы
и
эквивалентны тогда и только тогда, когда
и
. Класс эквивалентных мономорфизмов наз. под объектом объекта А. П. с представителем
иногда обозначают
или (m]. Допускается также возможность с помощью т. н. символа t Гильберта произвести выбор представителей подобъектов объекта Аи рассматривать этих представителей в качестве подобъектов. В категориях множеств, групп, абелевых групп, векторных пространств П. любого объекта определяется канонич. вложением подмножества (подгруппы, подпространства) в объемлющее множество (группу, пространство). Однако в категории тополо-гич. пространств введенное понятие П. шире понятия подмножества с индуцированной топологией.
Отношение предпорядка между мономорфизмами с общим концом Аиндуцирует отношение порядка между П. объекта
, если m<s. Это отношение аналогично отношению включения подмножеств некоторого множества.
Если мономорфизм m регулярен, то любой эквивалентный ему мономорфизм также регулярен. Поэтому можно говорить о регулярных П. любого объекта А. В частности, П. с представителем 1A регулярен. В категориях с нулевыми морфизмами аналогично вводятся нормальные П. Если в категории
существует бикатегорная структура
, то подобъект (m:X
А]объекта Аназ. допустимым (относительно указанной бикатегорной структуры), если
.
М. Ш. Цаленко.
Математическая энциклопедия. — М.: Советская энциклопедия.
.
1977—1985.
Полезное
Смотреть что такое «ПОДОБЪЕКТ» в других словарях:
-
подобъект технической эксплуатации — элемент технической эксплуатации — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия Синонимы элемент технической эксплуатации EN maintenance sub entityMSE … Справочник технического переводчика
-
АБЕЛЕВА КАТЕГОРИЯ — категория, обладающая рядом характерных свойств категории всех абелевых групп. А. к. были введены как основа абстрактного построения гомологич. алгебры (см. [4]). Категория наз. абелевой (см. [2]), если она удовлетворяет следующим аксиомам: А0.… … Математическая энциклопедия
-
ЛОКАЛИЗАЦИЯ — в категориях специальная конструкция, связанная со .специальными радикальными подкатегориями; она впервые появилась в абелевых категориях для описания т. н. Гротендика категорий с помощью категорий модулей над ассоциативными кольцами с единицей.… … Математическая энциклопедия
-
ОБРАЗ МОРФИЗМА — категории понятие, аналогичное понятию образа отображения одного множества в другое. Однако в теории категорий существует несколько подходов к определению этого понятия. Наиболее простой подход тесно связан с понятием би категории. Пусть в… … Математическая энциклопедия
-
ИДЕАЛ — специального рода подобъект в иек рой алгебраич. структуре. Понятие И. возникло первоначально в теории колец. Название И. ведет свое происхождение от идеальных чисел. Для алгебры, кольца или полугруппы Аидеал I есть подалгебра, подкольцо или… … Математическая энциклопедия
-
ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ ТЕОРИЯ — раздел дифференциальной геометрии, основанный на теории представления групп. Применение метода внешних дифференциальных форм позволяет ввести дифференциальные критерии Г. о. т., превращающие ее в эффективный аппарат дифференцпально геометрич.… … Математическая энциклопедия
-
ИНЪЕКТИВНЫЙ ОБЪЕКТ — такой объект I абелевой категории С, что для каждого мономорфизма а : отображение является сюръективным. Всякий инъективный подобъект I объекта А. выделяется прямым слагаемым. Произведение И. о. всегда И. о. В случае, когда каждый объект в… … Математическая энциклопедия
-
РЕТРАКТ — о б ъ е к т а к а т е г о р и и понятие, обобщающее соответствующие понятия алгебры и топологии. Объект Rкатегории наз. р е т р а к т о м объекта А, если существуют такие морфизмы что . Морфизм m при этом оказывается мономорфизмом и, более того,… … Математическая энциклопедия
-
ЯДРО — морфизма категории понятие, частными случаями к рого являются понятия ядра линейного преобразования векторных пространств, ядра гомоморфизма групп, колец и т. п. Пусть категория с нулевыми морфизмами. Морфизм наз. ядром морфизма если и всякий… … Математическая энциклопедия
-
Идеал (значения) — Идеал многозначный термин Идеал в философии и многих других областях представление о высшем совершенстве чего либо. Идеал (алгебра) специального рода подобъект в некоторой алгебраической структуре. Идеал село в Аларском… … Википедия
Транслитерация: Podobekt
Задом наперед читается как: ткеъбодоП
Подобъект состоит из 9 букв
рифмы к слову Подобъект,
слова из слова Подобъект,
слова начинающиеся на «По»,
слова начинающиеся на «Под»,
слова начинающиеся на «Подо»,
слова заканчивающиеся на «т»,
слова заканчивающиеся на «кт»,
слова заканчивающиеся на «ект»,
слова заканчивающиеся на «ъект»,
слова содеращие «од»,
слова содеращие «одо»,
слова содеращие «одоб»,
слова содеращие «одобъ»,
слова содеращие «одобъе»,
слова содеращие «одобъек»,
слова содеращие «одобъект»,
ПОДОБЪЕКТ
объекта категории — понятие, аналогичное понятию подструктуры математич. структуры. Пусть 












Отношение предпорядка между мономорфизмами с общим концом Аиндуцирует отношение порядка между П. объекта 
Если мономорфизм m регулярен, то любой эквивалентный ему мономорфизм также регулярен. Поэтому можно говорить о регулярных П. любого объекта А. В частности, П. с представителем 1A регулярен. В категориях с нулевыми морфизмами аналогично вводятся нормальные П. Если в категории 



М. Ш. Цаленко.
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей
и
примеров
предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных,
спряжению
глаголов, а также
морфемному строению слов.
Сайт оснащён мощной системой поиска с
поддержкой русской морфологии.
Разбор слова
по составу ОНЛАЙН
Подобрать синонимы
ОНЛАЙН
Найти предложения со словом
или
выражением ОНЛАЙН
Поиск по произведениям русской классики
ОНЛАЙН
Словарь афоризмов русских писателей
Подобъект
Материал из свободной энциклопедии
В теории категорий подобъект — это, грубо говоря, объект, который содержится в другом объекте категории. Определение обобщает более старые понятия подмножества в теории множеств и подгруппы в теории групп.[1] Поскольку «настоящее» строение объектов в теории категорий не рассматривается, определение опирается на использование морфизмов, а не «элементов».
Определение
Пусть A — объект некоторой категории. Имея два мономорфизма:
- u: S → A и
- v: T → A
с общим образом A, будем говорить что u ≤ v если u «пропускается через» v, то есть если существует морфизм w: S → T, такой что u = v ∘ w. Определим следующее бинарное отношение:
- u ≡ v тогда и только тогда, когда u ≤ v и v ≤ u.
Это отношение эквивалентности на мономорфизмах с образом A, назовём его классы эквивалентности подобъектами A. Мономорфизмы с образом A и отношением ≤ образуют предпорядок, но определение подобъекта гарантирует, что подобъекты A образуют частично упорядоченное множество.
Двойственное понятие к подобъекту — факторобъект; то есть, чтобы получить определение факторобъекта, нужно заменить в определении выше «мономорфизм» на «эпиморфизм» и поменять направление всех стрелок.
Примеры
В категории множеств подобъекты A соответствуют подмножествам A, или, точнее, классу всех вложений множеств, равномощных данному, в данное подмножество. То же верно в категории групп и в некоторых других категориях.
Примечания
- ↑ Mac Lane, p. 126
Литература
- Mac Lane, Saunders. Categories for the Working Mathematician. — 2nd. — New York, NY : Springer-Verlag, 1998. — Vol. 5. — ISBN 0-387-98403-8.

 — произвольная категория и А — фиксированный объект из
— произвольная категория и А — фиксированный объект из  . В классе всех мономорфизмов из
. В классе всех мономорфизмов из  с концом в Авводится отношение предпорядка (отношение делимости справа):
с концом в Авводится отношение предпорядка (отношение делимости справа):  предшествует
предшествует  или
или 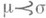 , если m=m’s для нек-рого
, если m=m’s для нек-рого  . В действительности, морфизм m’ однозначно определен, поскольку s — мономорфизм. Отношение предпорядка индуцирует отношение эквивалентности между мономорфизмами с концом в А:мономорфизмы
. В действительности, морфизм m’ однозначно определен, поскольку s — мономорфизм. Отношение предпорядка индуцирует отношение эквивалентности между мономорфизмами с концом в А:мономорфизмы 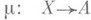 и
и 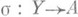 эквивалентны тогда и только тогда, когда
эквивалентны тогда и только тогда, когда  и
и 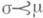 . Класс эквивалентных мономорфизмов наз. под объектом объекта А. П. с представителем
. Класс эквивалентных мономорфизмов наз. под объектом объекта А. П. с представителем  иногда обозначают
иногда обозначают 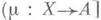 или (m]. Допускается также возможность с помощью т. н. символа t Гильберта произвести выбор представителей подобъектов объекта Аи рассматривать этих представителей в качестве подобъектов. В категориях множеств, групп, абелевых групп, векторных пространств П. любого объекта определяется канонич. вложением подмножества (подгруппы, подпространства) в объемлющее множество (группу, пространство). Однако в категории тополо-гич. пространств введенное понятие П. шире понятия подмножества с индуцированной топологией.
или (m]. Допускается также возможность с помощью т. н. символа t Гильберта произвести выбор представителей подобъектов объекта Аи рассматривать этих представителей в качестве подобъектов. В категориях множеств, групп, абелевых групп, векторных пространств П. любого объекта определяется канонич. вложением подмножества (подгруппы, подпространства) в объемлющее множество (группу, пространство). Однако в категории тополо-гич. пространств введенное понятие П. шире понятия подмножества с индуцированной топологией.  , если m<s. Это отношение аналогично отношению включения подмножеств некоторого множества.
, если m<s. Это отношение аналогично отношению включения подмножеств некоторого множества.  существует бикатегорная структура
существует бикатегорная структура  , то подобъект (m:X
, то подобъект (m:X А]объекта Аназ. допустимым (относительно указанной бикатегорной структуры), если
А]объекта Аназ. допустимым (относительно указанной бикатегорной структуры), если  .
.